 El martirio de Giordano Bruno y los infinitos mundos
El martirio de Giordano Bruno y los infinitos mundos
Las ideas materialistas de Lucrecio fueron recuperadas a inicios del siglo XV por el cardenal alemán Nicolás de Cusa. Éste sostuvo que el universo es infinito y por tanto no tiene centro, que la tierra no ocupa el centro del cosmos y que es semejante a otros planetas; desarrolló una filosofía panteísta –la idea de que Dios y la naturaleza son lo mismo–precursora del materialismo moderno: “Dios está en todas las cosas, de la misma manera que todas ellas están en él”.1 La estafeta heredada por Lucrecio, Cusa y Copérnico fue retomada por el fraile dominico Giordano Bruno en el siglo XVI, más de mil años después de Lucrecio.
La irreductible convicción sobre la infinitud del universo y la infinidad de mundos –algunos de ellos habitados por animales y seres inteligentes– que adornaban el cosmos, le costará a Giordano el destierro, ocho años de cárcel y finalmente morir en la hoguera de la Inquisición por su negativa a retractarse de sus ideas. Se mantuvo firme hasta el heroísmo, después de años de martirio desafió a sus jueces diciendo “Tembláis más vosotros al anunciar esta sentencia que yo de escucharla” 2 y se negó a besar el crucifijo que los monjes católicos le ofrecieron. El 17 de febrero de 1600 fue quemado vivo en la Plaza de Flores, en Roma. Su muerte y sus ideas nos abrieron las puertas de un universo infinito, puertas que, durante más de mil años, habían sido cerradas a la humanidad por el dogmatismo medieval. Otro más de los crímenes inenarrables de la Iglesia Católica.
Las primeras grietas en un mundo finito: Copérnico, Kepler, Galileo y Newton
“Si he llegado a ver más lejos que otros, es porque me subí a hombros de gigantes”
Newton
De acuerdo a la concepción de Ptolomeo el universo tenía como centro a una redonda pero corrupta tierra –algunos clérigos sostenían que la tierra era plana–; los planetas, el Sol y las estrellas giraban alrededor de la tierra unidos a esferas perfectas. “[Los planetas] no estaban sujetos directamente a las esferas sino indirectamente a través de una especie de rueda excéntrica. La esfera gira, la pequeña rueda entra en rotación, y Marte, visto desde la tierra, va rizando su rizo.”3 Este modelo permitía “explicar” el movimiento estelar y el aparentemente caprichoso movimiento excéntrico de los planetas. Pero los vientos frescos y revolucionarios del Renacimiento Europeo –impulsados por la acumulación originaria del capital, por el desarrollo de nuevas y más progresivas relaciones sociales– permitieron el acceso a fuentes clásicas griegas, a viejas tesis como la de Aristarco de Samos quien por primera vez sostuvo que la tierra giraba alrededor del Sol; Eratóstenes quien mil doscientos años antes del Renacimiento –solamente comparando el ángulo de las sombras proyectadas en el solsticio de verano por un poste en Alejandría y en un pozo en Siena–, había logrado la hazaña de medir la circunferencia terrestre; Apolonio de Pérgamo que antes que Kepler había afirmado que los planetas giraban alrededor del Sol siguiendo la elipse. Para algunos filósofos griegos la tierra era un planeta más en nuestro sistema y no el centro del universo.
En 1543 un clérigo polaco llamado Nicolás Copérnico recuperó la tesis heliocéntrica de los antiguos griegos –aunque se sabe que consultó a los antiguos, no los cita en su De revolutionibus orbium coelestium–. Si bien el modelo heliocéntrico permitía explicar mejor el movimiento de los seis planetas conocidos, atentaba contra los dogmas que habían reinado por más de mil años. El texto de Copérnico fue incluido, por la iglesia Católica, en las lista de los libros prohibido; lugar que ocupó hasta 1835. Incluso Martín Lutero condenó de forma insultante la tesis de Copérnico: “astrólogo advenedizo… Este estúpido quiere trastocar la ciencia astronómica. Pero la Sagrada Escritura nos dice que Josué ordenó pararse al Sol, y no a la tierra.”4 El debate sobre el lugar de la tierra en el cosmos no era para el orden establecido una discusión científica, sino un tema político e ideológico en el que no se podía ceder ni un palmo.
Kepler (un humilde maestro provinciano, estudioso de las matemáticas) se convirtió –después de la muerte del matemático Tycho Brahe, de quien había sido ayudante– en matemático imperial de Rodolfo II en Praga. Con base en las observaciones de los planetas legadas por Brahe, Kepler trató de explicar el movimiento aparentemente inexplicable de marte, incorporando la tesis herética de Copérnico. Al principio Kepler intentó tozudamente explicar el movimiento de marte mediante órbitas circulares ya que “la mente se estremece sólo de pensar en otra cosa […] sería indigno imaginar algo así en una creación organizada de la mejor manera posible.”5 Después de meses de desesperación y de haber probado con órbitas ovaladas y con ángulos diferentes, descubrió que la elipse encajaba a la perfección con las observaciones de su maestro. Kepler afirmó: “la verdad de la naturaleza, que yo había rechazado y echado de casa, volvió sigilosamente por la puerta trasera, y se presentó disfrazada para que yo la aceptara… ah, ¡qué pájaro más necio he sido!”.6 El descubrimiento de Kepler es aún más meritorio cuando se considera que intentó ser ministro protestante, era creyente de la astrología e, inicialmente, ferviente seguidor del sistema ptolemaico; pero pudo, a pesar de ello, remontarse sobre sus propios prejuicios y debelar la verdad, aunque ello significara –según sus propias palabras– “una cubetada de estiércol”; una que abriría de par en par un universo cerrado, mostrando que la tierra no era más que otro planeta girando en órbitas “imperfectas” alrededor del Sol.
Un mundo infinito se abría así ante las futuras generaciones. Galileo, inventor del telescopio, gran científico y matemático, escudriño un universo asombroso con ojos nuevos por primera vez en siglos. El impacto de encontrar que la Luna y el Sol tienen imperfecciones –cráteres, montañas lunares; manchas solares, las lunas de Júpiter, etc. – fue tal que cuando Galileo invitó a un clérigo a que mirara con sus propios ojos, éste dijo que las manchas estaban en sus ojos pero no en el Sol. Encontrar nuevos objetos celestes en un mundo cerrado removió prejuicios antiquísimos, alguno de sus detractores escribió: “Los astrólogos han hecho sus horóscopos teniendo en cuenta todo aquello que se mueve en los cielos. Por lo tanto los astros mediceos no sirven para nada y, Dios no crea cosas inútiles, estos astros no pueden existir”; en 1616 el Santo Oficio declara la teoría de Galileo como “una insensatez, un absurdo en filosofía, y formalmente herética.” No fue suficiente que los ciegos ojos de los clérigos observaran lo innegable, aun así Galileo fue obligado –en dos procesos, el primero firmado por el Papa Pablo V y el segundo por el Papa Urbano VIII, impulsados por el mismo cardenal que envió a la hoguera a Giordano Bruno– a retractarse de la tesis de que la tierra giraba alrededor del Sol o a sufrir torturas y prisión de por vida. Se retractó, pero se dice que desafiantemente le espetó a la Inquisición al final del proceso: “Eppur si muove” (sin embargo se mueve). El hombre que se había atrevido a mirar –en un mundo regido por ciegos– las montañas lunares y un el Sol que gira sobre su eje ligeramente inclinado, vivió sus últimos días de vejez bajo arresto domiciliario y completamente ciego; por lo menos pudo desquitarse de la inquisición publicando algunas de sus obras, pasadas de contrabando, en Francia y Estrasburgo. Aunque ciego, vio más lejos que nadie en su tiempo. Incluso Descartes renunció a publicar sus ideas atomistas por miedo a sufrir el destino de Galileo.
Kepler –apoyándose en Galileo– formuló tres leyes que gobernaban la traslación de los planetas alrededor del Sol. Newton, remontándose sobre los hombros de sus antecesores, vinculó esas leyes a otras más generales que serán conocidas como las tres leyes de la gravitación universal y que podrían las bases de la ciencia y de la mecánica por los siguientes doscientos cincuenta años. Gracias al conocimiento de estas leyes el hombre pudo poner sus pies en la luna cuyos cráteres Galileo observó con su telescopio por primera vez siglos atrás. Se demostró que las mismas leyes que gobiernan la caída de una manzana en la tierra, gobiernan el movimiento de los infinitos cuerpos celestes del universo. El universo cerrado del medioevo se hizo añicos para siempre, los cielos ya no eran más el reino inaccesible de Dios.
Sin embargo, todo avance –decía Engels– es a la vez un retroceso: aunque nuevamente la tierra fue integrada a un universo que se presentaba infinito, la concepción mecánica verá en el universo un simple mecanismo de relojería: rígido, repetitivo, sin vida y cuyo movimiento se tendía a explicar por la mano de un Dios que le dio cuerda.
El cálculo infinitesimal, lo infinitamente pequeño contenido en lo finito
Descartes, Leibniz y Newton, –a pesar del pensamiento mecánico dominante– se encontraron con el infinito nuevamente y, al mismo tiempo, con la dialéctica. El cálculo del movimiento siguiendo elipses que descubrió Kepler planteó a rajatabla la medición de curvas y sus tangentes. Descartes estudió el problema del cálculo de tangentes. El desarrollo de máquinas y la necesidad de la medición más exacta del movimiento mecánico obligaron a la búsqueda de nuevos sistemas matemáticos. La medición del movimiento en el tiempo y el espacio mecánicos llevó al plano cartesiano ideado por Descartes; la necesidad de medir la velocidad instantánea de un cuerpo, especialmente de un cuerpo siguiendo una trayectoria curvilínea, llevó a la necesidad de desarrollar el cálculo diferencial e integral, problema planteado inicialmente por Descartes.
Éste nuevo tipo de cálculo opera con cambios infinitamente pequeños representados en el plano cartesiano por funciones que Newton llamó “fluxiones” pero cuya argumentación era oscura. Leibniz creo –al mismo tiempo que Newton– un método más claro para medir la distancia entre curvas y sus tangentes manejando cantidades más pequeñas que cualquier número pero mayores que cero y, al mismo tiempo, considerando a esas pequeñas magnitudes iguales a cero con respecto a la integral. ¿Cómo era esto posible? ¿Cómo puede haber cantidades menores que cualquier número pero diferentes de cero? ¿Cómo se puede considerar una cantidad mayor que cero como nula o cero con respecto a su integral?
Aunque no es exactamente como fue explicado por sus fundadores, la diferenciación e integración consisten en calcular mediante funciones, magnitudes infinitesimales, necesarias para medir el área infinitamente pequeña debajo de una curva o para medir cualquier cambio mínimo con la mayor precisión posible –tanto el cálculo de áreas como de velocidades se pueden representar como el cálculo de áreas bajo la gráfica de una función, que es como se expresa gráficamente el cálculo diferencial e integral–. La integración consiste en sumar esos infinitos mínimos para “integrarlos” dentro de una magnitud infinitamente más grande en relación a esos números infinitesimales considerados iguales a cero en relación a su límite. El cálculo diferencial e integral va de lo infinito pequeño a un infinito mayor y a la inversa; cuando la función se integra ya no nos encontramos con la función inicial sino con una cualitativamente nueva que incorpora los cambios infinitesimales –que paradójicamente eran considerados como cero–. Implica al límite de una función como la parte finita de una relación, y la diferencial como la magnitud infinitamente pequeña contenida en esa magnitud finita. Así el cálculo infinitesimal lleva implícito –desde el punto de vista filosófico- la relación dialéctica –planteada en el plano matemático- de lo finito y lo infinito. Una relación de opuestos.
Actualmente el concepto geométrico de la derivada de una función se define como la pendiente de la recta tangente a la gráfica de la función en un punto x, por otra parte la integral de una función es el límite de la suma infinita de áreas infinitamente pequeñas. Si tenemos una función de posición, físicamente la derivada nos representa la velocidad de cambio en la posición, si tenemos una función que representa la velocidad e integramos obtenemos la función de posición; ambas operaciones son “opuestas” pero complementarias. Aunque la definición puede parecer obscura y abstracta para aquéllos que no estamos relacionados con el cálculo, lo que nos interesa aquí es explicitar las nociones de infinito e infinito implícitas al cálculo diferencial e integral. La noción de infinitesimal –de números infinitamente pequeños- desconcertó a los filósofos y matemáticos de aquellos tiempos y aún hoy desafía el sentido común. Hablamos de cantidades más pequeñas que cualquier número pero mayores que cero; cantidades que tienden a un límite pero nunca llegan a él por ser infinitamente pequeñas. Se planteó la necesidad de expresar de forma matemática rigurosa paradojas que Zenón había encontrado casi dos mil años antes.
Como siempre sucede, las mentes dogmáticas de esos tiempos no pudieron aceptar semejante sacrilegio. El obispo Berkeley condenó agriamente del nuevo sistema matemático –escribió que los infinitesimales no eran sino absurdos, “fantasma de cantidades que desaparecen”–7 su rotundo rechazo retrasó la amplia aceptación del nuevo cálculo necesario para la revolución industrial en ciernes. Marx, en contraste, no sólo se interesó en el estudio del cálculo diferencial e integral, sino que escribió interesantes cuadernos matemáticos donde concebía al cálculo infinitesimal como la medición de procesos –no de simples suma de magnitudes invariables– y de saltos dialécticos donde una cantidad finita se representa como sumas infinitas, donde el límite de primer orden puede presentarse como un diferencial infinitamente pequeño de una nuevo límite mayor; es decir, un proceso dialéctico que salta hacia nuevas magnitudes compuesta de nuevos infinitos. Cada vez que se integra la función nos encontramos en un caso de “negación de la negación”; es decir, con la misma función inicial –anterior a la diferenciación- que incorpora los pequeños cambios y que, por tanto, ya no es la misma una vez que se integra.8 Marx, en sus cuadernos matemáticos, ya mencionaba el concepto de límite que ni Newton ni Leibniz, más de cien años antes que él, comprendieron filosóficamente – concepto de límite que se desarrollaba casi al mismo tiempo que Marx escribía dichos cuadernos, no serán publicados sino hasta 1968–. Marx –y su compañero de armas Engels- tuvo siempre una actitud crítica e independiente de los grandes descubrimientos científicos de su tiempo, incluidas las matemáticas: “[…] comenzando con el método místico de Newton y Leibniz; pasando luego al método racionalista de D Alembert y Euler; para terminar finalmente con el método estrictamente algebraico (pero partiendo siempre de la misma concepción fundamental propia de Newton y Leibniz) de Lagrange. […]”9
Aunque las contradicciones implícitas en el cálculo diferencial e integral trataron de ser ocultadas e ignoradas por posteriores formulaciones como las del francés Louis de Cauchy, nuevos planteamientos como los de Abraham Robinson –presentados a mediados del siglo XX– han sacado de nuevo a la luz estas contradicciones, de acuerdo a su abordaje: “cada número real, identificado con un punto sobre una recta, posee alrededor de él una especie de nube electrónica de infinitesimales más pequeños que cualquier número.”10 Estos números son llamados “número reales no estándar” con sus leyes y propiedades específicas.
¿Acaso el cálculo diferencial e integral y los infinitos que incluye son sólo una especie de reglas arbitrarias útiles para realizar operaciones pero que no tienen nada que ver con la realidad, una especie de reglas en un juego de mesa matemático? Si el Cálculo diferencial e integral se aplica a la realidad eficientemente es sólo porque expresa algo de esa realidad. Engels explica que la diferenciación y la integración son procesos que se dan en la naturaleza, los cuales han sido abstraídos por el cálculo y aplicados nuevamente a la realidad, razón por la cual el cálculo se verifica en ella. Engels escribe: “[…] de todos los progresos teóricos nos hay seguramente ninguno que sea un triunfo tan elevado del espíritu humano como el descubrimiento del cálculo infinitesimal, en la segunda mitad del siglo XVII. Si existe una proeza pura y exclusiva de la inteligencia humana, hela aquí. El misterio que aún hoy rodea a las magnitudes empleadas en el cálculo infinitesimal-las diferenciales y los infinitos de diversos grados-, es la mejor prueba de que todavía que aquí tenemos que manejarnos con puras creaciones e imaginaciones libres del espíritu humano, sin equivalente alguno en el mundo objetivo. Y, sin embargo, la verdad es a la inversa. La naturaleza nos ofrece los prototipos de todas estas magnitudes imaginarias. Nuestra geometría toma como punto de partida las relaciones espaciales; nuestra aritmética y álgebra, las magnitudes numéricas, que corresponden a nuestras condiciones terrenales y, por ende, a las magnitudes de los cuerpos que la mecánica llama masas; masas, tal como se presentan en la tierra y tal como son movidas por los hombres. Comparativamente a estas masas, la masa de la tierra parece ser infinitamente grande y, precisamente, es tratada como infinitamente grande por la mecánica terrestre. El radio terrestre = ∞ [infinito], éste es el principio fundamental de toda la mecánica en la ley de la gravedad. Pero no sólo la tierra, sino el sistema solar entero y las distancias dadas en él, aparece a su vez como infinitamente pequeñas no bien nos ocupamos de las distancias, estimables en años luz, que hayamos en los sistemas estelares visibles a nosotros a trevés del telescopio. De manera que ya tenemos aquí un infinito no sólo de primer grado, sino de segundo, y dejamos a la fantasía de nuestros lectores la tarea de construir en el espacio sin fin sucesivos infinitos de grado superior, si se sienten inclinados a ello .” Aunque el cálculo diferencial reintegró el infinito a las matemáticas, éste trabaja con funciones regulares y continuas , por lo que no son adecuadas para describir patrones donde no es posible trazar una tangente a la curva. Más adelante hablaremos de las estructuras fractales que además de ser no diferenciables incorporan de nuevo la noción de infinito.
El Hotel de Hilbert y los infinitos diversos de Cantor
La certeza dialéctica, que sostuvieron Engels y Marx en el “Anti-Dühring”, de que el universo está colmado de infinitos de diversos grados, fue demostrada matemáticamente por el matemático alemán Georg Cantor en 1870. Anterior a él, Euclides ya había señalado que hay infinitos números primos, Galileo había establecido una curiosa paradoja relativa al infinito: existen tantos números pares como números naturales ya que ambos son infinitos –es posible aparear o relacionar entre sí, uno a uno, cada uno de los elementos que componen ambos conjuntos–, violando el principio lógico formal que afirma que el todo es igual a la suma de sus partes y que la parte es siempre menor que el todo.
Dicen los matemáticos que tres manzanas y tres personas tienen la misma cardinalidad porque es posible equiparar cada miembro del conjunto de las tres manzanas con cada miembro de conjunto de las tres personas. En 1850 el teólogo alemán Bernhard Bolzano demostró que dos intervalos, independientemente de sus longitudes, siempre tienen la misma cardinalidad. Efectivamente: es posible encontrar para cada número de una recta infinita otro punto equivalente de una recta finita, de tal modo que una recta finita tiene literalmente infinitos puntos, tantos como una recta sin fin. El lector puede hacer el experimento gráfico si lo desea: simplemente –como se muestra en la imagen– se traza una línea tan larga como se quiera (supongámosla infinita) de tal forma que sea tangente de un círculo finito. Con este esquema se puede trazar una línea que parta de la línea infinita y que, llegando al punto superior al círculo, una a otro punto equivalente del perímetro del círculo; demostrando con ello que en el perímetro finito del círculo hay tantos puntos como en la recta infinita. Ambas tienen la misma cardinalidad, es decir, es posible aparear, uno a uno, tantos puntos distintos de un conjunto, con otros tantos puntos equivalentes de otro conjunto. Si no es posible hacer esto para dos conjuntos cualquiera, se dice que ambos tienen cardinalidad diferente, ya sea mayor o menor según el caso.
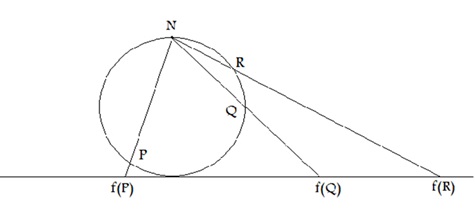
Lo paradójico del esto es que aunque es claro que una recta infinita tiene mayor longitud que una recta finita, ambas tienen la misma cardinalidad, la misma cantidad de puntos. La matemática se volvió a encontrar con la paradoja de la dicotomía de los viejos eleatas. En realidad, desde el punto de vista dialéctico, no debería sorprendernos que en una magnitud finita haya infinitos ocultos: si asumimos que una magnitud es sólo una parte integrante del infinito, entonces cualquier segmento debe también ser infinito, o de lo contrario el infinito encontraría su fin o su principio. La conclusión es que el infinito está implícito en lo finito y a su vez –como Engels escribió– el infinito está compuesto de innumerables magnitudes finitas: “La infinitud es una contradicción y está llena de contradicciones. Ya es una contradicción el que una infinitud tenga que estar compuesta de honradas finitudes, y, sin embargo, tal es el caso. La limitación del mundo material lleva a no menos contradicciones que su ilimitación, y todo intento de eliminar esas contradicciones, lleva a nuevas y peores contradicciones: Precisamente porque la infinitud es una contradicción, es infinita, un proceso que se desarrolla sin fin en el espacio y en el tiempo. La superación de la contradicción sería el final de la infinitud.”12
Un ejemplo clásico para demostrar la cardinalidad de diferentes magnitudes en su relación al infinito –para demostrar que existen infinitos mayores y menores– es el experimento mental ideado por el famoso matemático alemán de fines del siglo XIX: David Hilbert. El experimento es conocido como “El hotel de Hilbert”, con éste, Hilbert ejemplificó las propiedades paradójicas del infinito que Cantor había estudiado. Aunque se trata de un ejercicio mental –ejercicio del que muchas veces se abusa en la ciencia ficción para sostener todo tipo de hipótesis arbitrarias– es útil al ejemplificar, de forma más accesible e intuitiva, las paradojas y la dialéctica del infinito.
Se supone que en la recepción de un hotel de infinitas habitaciones, que está a su máxima capacidad, llega un individuo buscando hospedaje. El sentido común nos dice que es imposible encontrar habitación en un hotel absolutamente lleno, pero el infinito tiene propiedades que violan la lógica formal: el recepcionista invita a los huéspedes del hotel que sumen la unidad al número de su habitación y se muden a la habitación marcada con el número resultante: el huésped de la habitación 1 se pasará al 2, el 2 al 3 y así hasta el infinito. Como el infinito no tiene fin, esta operación es posible y el nuevo huésped encuentra habitación. Cuando un grupo de infinitos huéspedes se presenta a la recepción buscando hospedaje, un nuevo desafío se le presenta al recepcionista del hotel de infinitas habitaciones. El recepcionista no se inmuta e invita a los huéspedes que ocupan las infinitas habitaciones a que multipliquen por dos el número de su habitación y se muden a las nuevas habitaciones marcadas con el número resultante. Es claro que todos los huéspedes se mudarán a las habitaciones con números pares; dado que la cantidad de números pares es infinita es posible hacer esa operación y los nuevos huéspedes ocuparán las habitaciones nones vacías sin problema alguno dado que los números nones son también infinitos. Otro desafío aún mayor –¡un desafío infinito!- se le presentó al recepcionista cuando llegaron a la recepción un número infinito de camiones, cada uno con un número infinito de personas buscando habitación. Al recepcionista no se le tensó ni un músculo de la cara. Lo que hizo fue comunicarse con los huéspedes hospedados en habitaciones con número primo (distinto de 1) y a las habitaciones cuyo número de habitación fuera resultado de una potencia de un número primo, pidiéndoles que hicieran la operación consistente en elevar el número 2 a la potencia del número de su habitación y que se mudarán a la habitación numerada con el resultado de esa potencia. Entonces el recepcionista asigno a cada uno de los infinitos camiones, cada uno de los números primos (distintos de 1); luego asigno a cada una de las infinitas personas de cada uno de los infinitos camiones un número impar diferente y les pidió elevar ese número impar a la potencia del número primo que le correspondió a su camión. Dado que existen infinitos números impares e infinitos números primos es posible incluir infinitos grupos de infinitos miembros dentro de un hotel infinito. El Hotel de Hilbert es un experimento que deja claro que existen diversos grados de infinitos –mayores y menores, transfinitos de otros finitos menores– que, no obstante ser mayores o menores, tienen la misma cardinalidad. Lo cual es una contradicción dialéctica tan cierta como lo es la recta de los números naturales.
Cantor, quien inspiró “el hotel de Hilbert”, sistematizó las propiedades del infinito por medio de la llamada “Teoría de conjuntos”, no sólo confirmó que diversos infinitos –a pesar de ser mayores o menores– tienen la misma cardinalidad (mostró que los números enteros tienen la misma cardinalidad que los naturales y que los racionales) – lo que ya es de por sí asombroso–, sino que demostró que hay infinitos que no tienen la misma cardinalidad, que existen infinitos tipos de infinitos; de paso, mostró que las propiedades del infinito no se ajustan a la lógica formal aristotélica. El fractal que lleva su nombre –“El polvo de Cantor” (al que volveremos más adelante) – demuestra, por ejemplo, no sólo que las propiedades del infinito no cumplen el axioma Euclidiano y Aristotélico de que el todo es mayor que sus partes, sino que hay casos concretos donde la parte es mayor que el todo. Los fractales son estructuras geométricas que se repiten a sí mismas dentro de su propia estructura. En el fractal descubierto por Cantor, el todo tiende a cero mientras que las partes son infinitas. Es un fractal compuesto por una línea tan infinitamente fragmentada que su longitud tiende a cero pero los puntos que la componen son infinitos, es decir que la parte es mayor que el todo.
Cantor demostró –como hemos señalado- que hay infinitos con distinta cardinalidad. La manera en que lo hizo es simple pero genial, se le conoce como razonamiento diagonal. Consideró el conjunto de los números reales –los números que tienen una expansión decimal racional e irracional– para hacer una lista que se supone completa y luego aparear uno a uno este conjunto con el de los números naturales. El profesor Fausto Ongay explica el procedimiento13que se ilustra más abajo: “Supongamos que […] hemos logrado establecer una lista que incluya todas las expresiones decimales [y que hemos apareado uno a uno todos los números de esta lista con los infinitos números naturales; suponiendo, así, que poseen la misma cardinalidad]. Entonces podemos construir [infinitos dígitos con su expansión decimal que no estén incluidos en esa lista, y por tanto que no hayan sido considerados en su apareamiento con el conjunto de los números naturales] de la forma siguiente: [trazamos una diagonal cualquiera a la lista de los números reales que hemos establecido y con la ayuda de esa diagonal formamos un nuevo dígito con su expresión decimal] para la primera de las expansiones de la lista escogemos un dígito distinto de su primer dígito; para la segunda uno distinto del segundo dígito, para la tercera uno distinto del tercero, y así ad infinitum. Es claro que escribiendo en orden estos dígitos obtenemos la expansión decimal de un número. Pero también es bastante claro que esta expansión no está en la lista […] de este modo, el infinito de los números reales ¡es mayor que el de los naturales! [Y, además, los números reales tienen una cardinalidad diferente que no es posible aparear con los números naturales ya que siempre faltarían números a la lista de los números reales].”14 De esta manera Cantor descubrió que existen diferentes e infinitos tipos de infinitos, con características y cadinalidades diversas. Esto es, en esencia, lo que sostenía Engels.

Cantor tuvo una vida trágica, desde 1884 fue internado intermitentemente en instituciones mentales, hay quien señala que como resultado de las contradicciones lógicas descubiertas con su estudio del infinito o por el hecho de que sus resultados fueron rechazados por la ortodoxia matemática de su tiempo y entraban en contradicción con su educación religiosa. Sin embargo, sus contribuciones son hoy ampliamente reconocidas por la matemática moderna, resultados que reivindican y profundizan la compresión dialéctica del infinito.
_____________
NOTAS
1. Dynnik, Historia de la filosofía, Tomo I, Grijalbo, México, 1962, p. 265.
2. Dynnik, Historia de la filosofía, Tomo I, Grijalbo, México, 1962, p. 289.
3. Sagan, Carl; Cosmos, Planeta, Madrid, 1985, p. 51.
4. Sagan, Carl; Cosmos, Planeta, Madrid, 1985, p. 53.
5. Sagan, Carl; Cosmos, Planeta, Madrid, 1985, p. 60.
6. Sagan, Carl; Cosmos, Planeta, Madrid, 1985, p. 61.
7. Ongay, Fausto, Mathema, el arte del conocimiento, FCE, México, 2000, pp. 66-67.
8. Cf. Marx, Carl, “Sobre el concepto de derivada de una función (manuscrito 4147)”, UAM, México, 1997.
9. Carta de Marx a Engels, 22 de noviembre de 1882.
10. Ongay, Fausto, Mathema, el arte del conocimiento, FCE, México, 2000, pp. 67.
11. Engels, “Notas al anti-Dühring”, en La génesis del Anti-Düring, Roca, México, 1975, p.85.
12. Engels, Anto-Dühring, Grijalbo, México, 1975, p. 39.
13. Nos hemos tomado la licencia de completar su argumentación –entre corchetes- para hacerla lo más clara posible ya que puede resultar un tanto abstracta u oscura para aquéllos que no estamos relacionados con el tema, esperamos no haber violentado demasiado su texto.
14. Ongay, Fausto, Mathema: El arte del conocimiento, FCE, México, 2000, pp. 77-78.






